Problem Questions with Answer, Solution | Mathematics - Exercise 9.3: Applications of limits | 11th Mathematics : UNIT 9 : Differential Calculus Limits and Continuity
Chapter: 11th Mathematics : UNIT 9 : Differential Calculus Limits and Continuity
Exercise 9.3: Applications of limits
EXERCISE 9.3

(9) An important problem in fishery science is to estimate the number of fish presently spawning in streams and use this information to predict the number of mature fish or “recruits” that will return to the rivers during the reproductive period. If S is the number of spawners and R the number of recruits, “Beverton-Holt spawner recruit function” is R(S) = S / (α S + β ) where α and β are positive constants. Show that this function predicts approximately constant recruitment when the number of spawners is sufficiently large.
(10) A tank contains 5000 litres of pure water. Brine (very salty water) that contains 30 grams of salt per litre of water is pumped into the tank at a rate of 25 litres per minute. The concentration of salt water after t minutes (in grams per litre) is C(t) = 30t / 200+t
What happens to the concentration as t →∞?
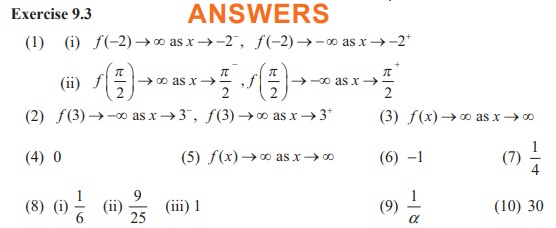







Related Topics