Exercise 5.4: Tangents and Normals to Conics

EXERCISE 5.4

1. Find  the  equations  of  the  two  tangents that can be drawn from (5, 2) to the ellipse 2x2 + 7 y2 = 14 .

2. Find the equations of tangents to the hyperbola 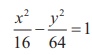 which are parallel to 10x − 3y + 9 = 0.

3. Show that the line x − y + 4 = 0 is a tangent to the ellipse x2 + 3y2 = 12 . Also find the coordinates of the point of contact.

4. Find the equation of the tangent to the parabola y2 = 16x perpendicular to 2x + 2 y + 3 = 0 .

5. Find the equation of the tangent at t = 2 to the parabola y2 = 8x . (Hint: use parametric form)

6. Find the equations of the tangent and normal to hyperbola 12x2 − 9 y2 = 108 at θ = π/3. (Hint: use parametric form)

7. Prove that the point of intersection of the tangents at ‘ t1 ’ and ‘ t2 ’on the parabola y2 = 4ax is [at1t2 , a (t1 + t2 )]. 

8. If the normal at the point ‘ t ’ on the parabola y2 = 4ax meets the parabola again at the point  ‘ t ’, then prove that t2= - ( t + 2/t1).

Answers: