Problem Questions with Answer, Solution | Complex Numbers - Exercise 2.8: de MoivreŌĆÖs Theorem and its Applications | 12th Mathematics : UNIT 2 : Complex Numbers
Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
Exercise 2.8: de MoivreŌĆÖs Theorem and its Applications
EXERCISE 2.8
1. If Žē ŌēĀ 1 is a cube root of unity, show that 

2. Show that 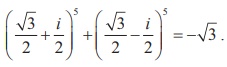

3. Find the value of 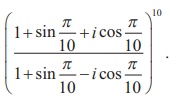

4. If 2cos╬▒ = x + [1/x] and 2cos ╬▓ = y + [1/y] , show that
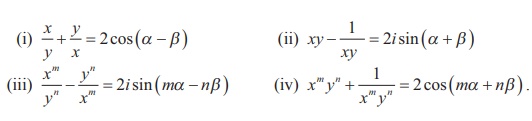


5. Solve the equation z3 + 27 = 0 .
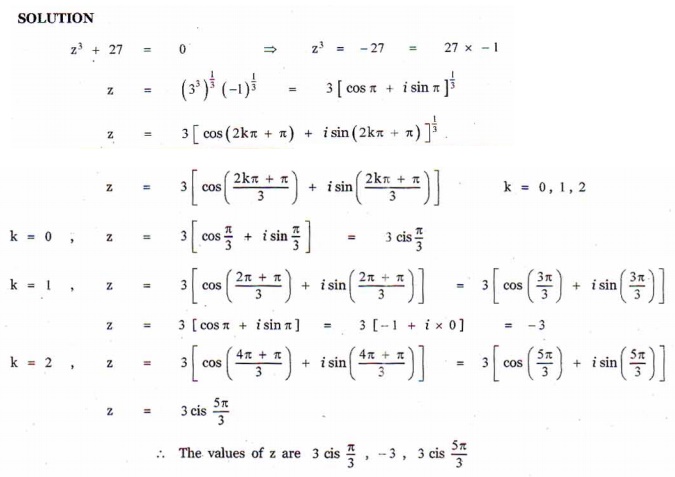
6. If Žē ŌēĀ 1 is a cube root of unity, show that the roots of the equation ( z -1)3 + 8 = 0 are -1, 1- 2Žē, 1- 2Žē2 .

7. Find the value of 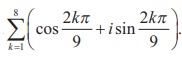

8. If Žē ŌēĀ 1 is a cube root of unity, show that
(i) (1- Žē + Žē2)6 + (1+ Žē - Žē2 )6 = 128.
(ii) (1+ Žē )(1+ Žē2)(1+ Žē4 )(1+ Žē8 )... ...(1+ Žē 2.pow(11) ) = 1.

9. If z = 2 - 2i , find the rotation of z by ╬Ė radians in the counter clockwise direction about the origin when
(i) ╬Ė = ŽĆ/3
(ii) ╬Ė = 2ŽĆ/3
(iii) ╬Ė = 3ŽĆ ./2

10. Prove that the values of 4ŌłÜ-1 are ┬▒ 1/ŌłÜ2 (1┬▒i).
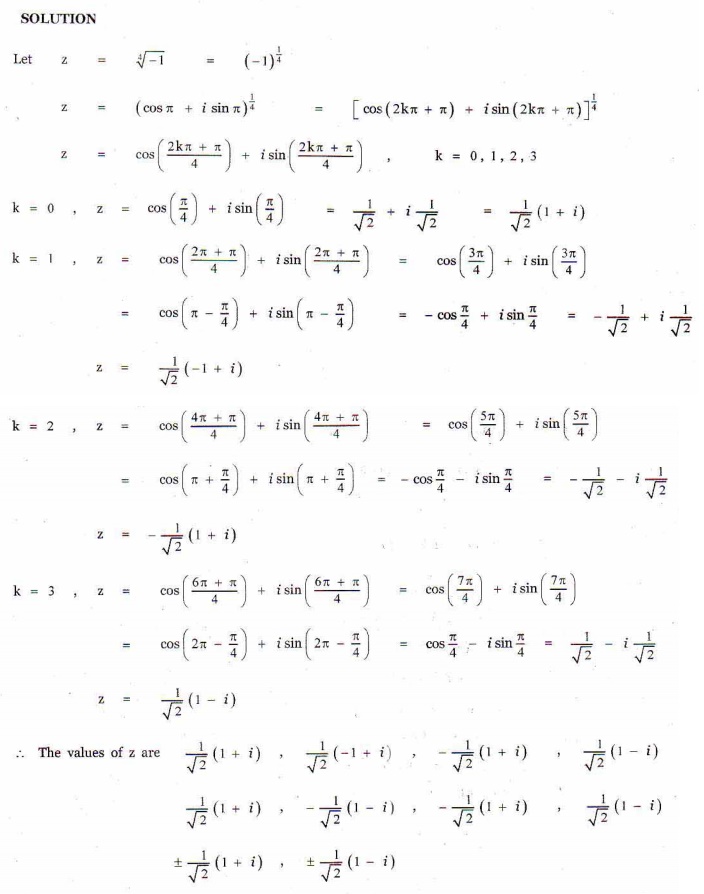
Answers:
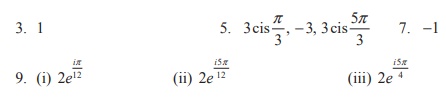
Related Topics