Problem Questions with Answer, Solution - Exercise 11.5: Theoretical Distributions: Some Special Discrete Distributions | 12th Maths : UNIT 11 : Probability Distributions
Chapter: 12th Maths : UNIT 11 : Probability Distributions
Exercise 11.5: Theoretical Distributions: Some Special Discrete Distributions
EXERCISE 11.5
1. Compute P ( X = k) for the binomial distribution, B ( n , p) where
(i) n = 6, p = 1/3, k = 3 (ii) n = 10, p = 1/5 , k = 4 (iii) n = 9, p = 1/2 , k = 7

2. The probability that Mr.Q hits a target at any trial is 1/4 Suppose he tries at the target 10 times. Find the probability that he hits the target (i) exactly 4 times (ii) at least one time.

3. Using binomial distribution find the mean and variance of X for the following experiments
(i) A fair coin is tossed 100 times, and X denote the number of heads.
(ii) A fair die is tossed 240 times, and X denote the number of times that four appeared.
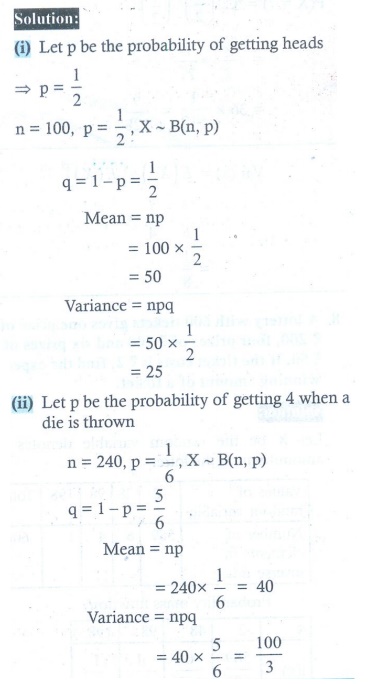
4. The probability that a certain kind of component will survive a electrical test is 3/4 . Find the probability that exactly 3 of the 5 components tested survive.

5. A retailer purchases a certain kind of electronic device from a manufacturer. The manufacturer indicates that the defective rate of the device is 5%.
The inspector of the retailer randomly picks 10 items from a shipment. What is the probability that there will be (i) at least one defective item (ii) exactly two defective items?

6. If the probability that a fluorescent light has a useful life of at least 600 hours is 0.9, find the probabilities that among 12 such lights
(i) exactly 10 will have a useful life of at least 600 hours;
(ii) at least 11 will have a useful life of at least 600 hours;
(iii) at least 2 will not have a useful life of at least 600 hours.

7. The mean and standard deviation of a binomial variate X are respectively 6 and 2.
Find (i) the probability mass function (ii) P( X = 3) (iii) P( X ≥ 2) .

8. If X ~ B(n, p) such that 4P( X = 4) = P( X = 2) and n = 6 . Find the distribution, mean and standard deviation of X.

9. In a binomial distribution consisting of 5 independent trials, the probability of 1 and 2 successes are 0.4096 and 0.2048 respectively. Find the mean and variance of the random variable.
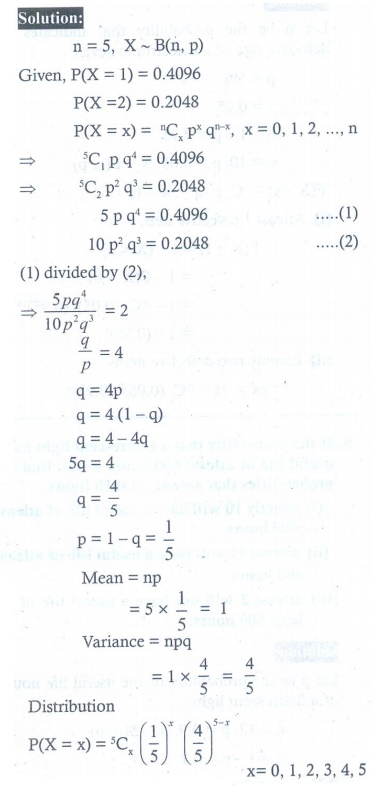
Answers:
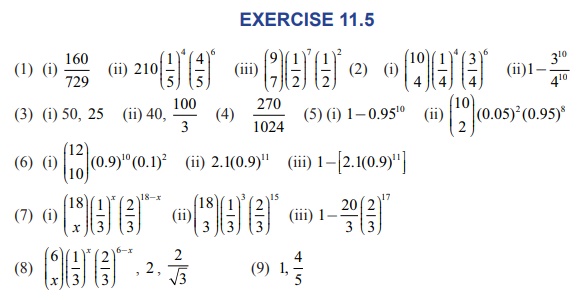
Related Topics