Problem Questions with Answer, Solution - Exercise 1.6: Matrix: Non-homogeneous Linear Equations | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Exercise 1.6: Matrix: Non-homogeneous Linear Equations
EXERCISE 1.6
1. Test for consistency and if possible, solve the following systems of equations by rank method.
(i) x - y + 2z = 2, 2x + y + 4z = 7, 4x - y + z = 4
(ii) 3x + y + z = 2, x - 3y + 2z = 1, 7x - y + 4z = 5
(iii) 2x + 2 y + z = 5, x - y + z = 1, 3x + y + 2z = 4
(iv) 2x - y + z = 2, 6x - 3y + 3z = 6, 4x - 2y + 2z = 4




2. Find the value of k for which the equations kx - 2 y + z = 1, x - 2ky + z = -2, x - 2 y + kz = 1 have
(i) no solution
(ii) unique solution
(iii) infinitely many solution


3. Investigate the values of λ and μ the system of linear equations 2x + 3y + 5z = 9, 7x + 3y – 5z = 8, 2x + 3y + λ z = µ , have
(i) no solution (ii) a unique solution (iii) an infinite number of solutions.

Answers:
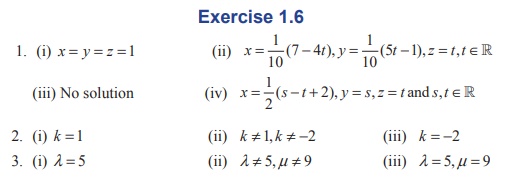
Related Topics