Answer the following questions

MOTION

TEXT BOOK EXERCISES

VI. Answer briefly:

1. Define velocity.

Answer:

(i) Velocity is the rate of change of displacement. It is the displacement with unit time. It is a vector quantity. The SI unit of velocity is ms^-1.

(ii) Thus, Velocity = Displacement / time taken.

2. Distinguish distance and displacement.

Answer.

Distance

1. The actual length of the path travelled by a moving body irrespective of the direction

2. It is a Scalar quantity

Displacement

1. The change in position of a moving body in a particular direction

2. It is a Vector quantity

3. What do you mean by uniform motion?

Answer.

An object is said to be in uniform motion if it covers equal distances in equal intervals of time howsoever big or small these time intervals may be.

4. Compare speed and velocity.

Answer.

Speed

1. It is the rate of change of distance with respect to time

2. It is a scalar quantity having magnitude only

3. Speed is velocity without a particular direction

4. It is measured in ms^-1 in SI system

5. Speed in any direction would be a positive quantity, since the distance in any direction is a positive quantity.

Velocity

1. It is the rate of change of displacement with respect to time

2. It is a vector quantity having both magnitude and direction

3. Velocity is speed in a particular direction

4. It is also measured in ms^-1 in a particular direction in SI system

5. Velocity can get both positive and negative values. If velocity in one direction is assumed to be positive then the velocity in the opposite direction would be a negative quantity. Velocity can get zero value also.

5. What do you understand about negative acceleration?

Answer:

If velocity decreases with time the value of acceleration is negative.

Note: Negative acceleration is called retardation or deceleration.

6. Is the uniform circular motion accelerated? Give reasons for your answer.

Answer:

When an object is moving with a constant speed along a circular path, the change in velocity is only due to the change in direction. Hence it is accelerated motion.

7. What is meant by uniform circular motion? Give two examples of uniform circular motion.

Answer:

When an object moves with constant speed along a circular path, the motion is called uniform circular motion.

Example:

1. The Earth moves around the Sun in the uniform circular motion.

2. The Moon moves in uniform circular motion around the Earth.

VII. Answer in detail:

1. Derive the equations of motion by graphical method.

Answer:

Equations of motion from velocity - time graph:

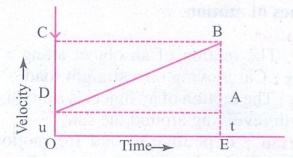
 Graph shows the change in velocity with time of a uniformly accelerated object. The object starts from the point D in the graph with velocity u. Its velocity keeps increasing and after time t it reaches the point B on the graph.

The initial velocity of the object = u = OD = EA

The final velocity of the object = v = OC = EB

Time = t = OE = DA

Also from the graph we know that, AB = DC

1. First equation of motion:

By definition, acceleration = change in velocity / time

= (final velocity − initial velocity) / time

= (OC−OD)/OE

 a = DC/OE

a = DC / t

DC = AB = at

From the graph EB = EA + AB

 v = u + at      ………(1)

This is first equation of motion.

2. Second equation on of motion:

From the graph the distance covered by the object during time t is given by the area of quadrangle DOEB

s = area of the quadrangle DOEB

= area of the rectangle DOEA + area of the triangle DAB

= (AE × OE) + (l/2 × AB × DA)

s = ut + 1/2(at²) …………(2)

This is the second equation of motion.

3. Third equation of motion:

From the graph the distance covered by the object during time t is given by the area of the quadrangle DOEB. Here DOEB is a trapezium. Then,

 s = area of trapezium DOEB

 = 1/2 × sum of length of parallel side × distance between parallel sides

= 1/2 × (OD+BE) × OE

S=1/2×(u+v) × t

Since a = ( v - u )/ t or t =( v - u ) / a

Therefore s = 1/2 × ( v + u ) × ( v – u ) / a

2as = v^{2 _} u²

 v² = u² + 2 as ……….(3)

This is the third equation of motion.

2. Explain different types of motion.

Answer:

Different types of motion:

(i) Linear motion: The motion of an object along a straight line is known as linear motion. Ex: Car moving on a straight road.

(ii) Circular motion: The motion of an object is a circular path is known as circular motion. Ex: Earth revolving around the sun.

(iii) Oscillatory motion: Repetitive to and fro motion of an object at regular interval of time is called as oscillatory motion. Ex: Motion of pendulum of a clock.

(iv) Random motion: The disordered or irregular motion of a body is called random motion. Ex: Movement of fish under water.

VIII. Exercise Problems:

1. A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10ms^-2, with what velocity will it strike the ground? After what time will it strike the ground?

Answer:

Here we have

Initial velocity, u = 0

 Distance, s = 20 m

Acceleration, a = 10m/s²

Final velocity, v = ?

 Time,t = ?

a) Calculation of final velocity, v

 We know that, v² = u² + 2as

 v² = 0+2 ×10 m/s ² × 20m

 v² = 400 m²/s²

 =√ [400m² /s² ]

 v = 20 m/s

b) Calculation of time, t

We know that, v = u + at

 20 m/s = 0+10 m/s² × t

 t = (20m/s²) / (20m/s) =2s

∴ Ball will strike the ground at a velocity of 20 ms⁻¹

Time taken to reach the ground = 2s.

2. An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 m and 20 s?

Answer: Here we have

 Diameter = 200 m

 ∴ Radius = 200 m/2 = 100 m

Time of one rotation = 40 s

Time after 2m 20 s = 2 × 60 s + 20 s = 140s

Distance after 140s = ?

Displacement after 140s =?

Circular track with diameter of 200m

We know that, velocity along a circular path = circumference / time

 v = 2πr / 40s

 v = [2 × 3.14 × 100m] / 40s

 v = 628m /40s

 v = 15.7 m/s

a) Distance after 140 s

We know that, distance = velocity × time

 Distance = 15.7m/s × 140s

 = 2198 m

b) Displacement after 2 min 20 s i.e, in 140 s

We know that, distance = velocity × time

Since, rotation in 40s = 1

∴ Rotation in 1s = 1/ 40

∴ Rotation in 140 s = 1/40 × 140 = 3.5

∴ In 3.5 rotation athlete will be just at the opposite side of the circular track.

i.e. at a distance equal to the diameter of the circular track which is equal to 200m

∴ Distance covered in 2min 20 s = 2198 m

Displacement after 2min 20s = 200 m

3, A racing car has a uniform acceleration of 4ms⁻². What distance it covers in 10s after the start?

Answer:

Here we have

Acceleration, a = 4 m/s²

Initial velocity u = 0

Time t = 10 s

Distance (s) covered = ?

We know that, s = ut +1/2 at²

s = (0×10s) + [l/2×4m/s² × (10 s)² ]

= 1/2 × 4 m/s² × 100s²

= 2 × 100m = 200 m

Thus, racing car will cover a distance of 200 m after start in 10s with given acceleration. 

Intext Activities

ACTIVITY - 1

Look around you. You can see many things: a row of houses, large trees, small plants, flying birds, running cars and many more. List the objects which remain fixed at their position and the objects which keep on changing their position.

Solution:

1. Row of houses, large trees, small plants are the examples, of immovable objects.

2. Flying birds, running cars and buses are the examples of movable objects.

Activity to be done by the students themselves

ACTIVITY-2

Tabulate the distance covered by a bus in a heavy traffic road in equal intervals of time and do the same for a train which is not in an accelerated motion. From your table what do you understand?

The bus covers unequal distance in equal intervals of time but the train covers equal distances in equal intervals of time.

Solution:

ACTIVITY - 3

Observe the motion of a car as shown in the figure and answer the following questions:

Compare the distance covered by the car through the path ABC and AC. What do you observe?

Which path gives the shortest distance to reach D from A? Is it the path ABCD or the path ACD or the path AD?

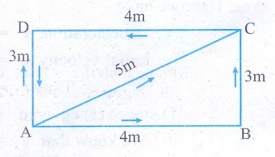
Solution:

1. Distance covered by the car through the path ABC = 4m + 3m = 7 m. and AC = 5 m. The distance covered by the car through the path ABC is large compared to AC.

2. The shortest distance to reach D from A is path AD = 3m.

3. The total distance covered by the car ABCDA = 14 m. It finally reaches to A. 

ACTIVITY - 4

Take a large stone and a small eraser. Stand on the top of a table and drop them simultaneously from the same height? What do you observe? Now, take a small eraser and a sheet of paper. Drop them simultaneously from the same height. What do you observe? This time, take two sheets of paper having same mass and crumple one of the sheets into a ball. Now, drop the sheet and the ball from the same height. What do you observe?

Solution:

Both the stone and the eraser have reached the surface of the Earth almost at the same time.

The eraser reaches first and the sheet of paper reaches later.

The paper crumpled into a ball reaches ground first and plain sheet of paper reaches later, although they have equal mass. It is because of air resistance. The magnitude of air resistance despends on the area of object exposed to air. So the sheet of paper reaches later.